Lab 2: Dot to Dot Generator

Learning Outcomes

• Implement algorithms using both ArrayLists and LinkedLists.

Resources

• Video introduction

Overview

This week you will implement an algorithm to reduce the number of dots in the picture so that more reasonable dot to dot challenges can be created.

Assignment

Your program must:

• Incorporate feedback from your instructor from lab 1.
• Indicate the total number of dots in the selected file.
• Add a menu item called Number of Dots that will allow the user to enter a desired number of dots.
• Display the picture produced by removing all but the user-specified number of dots.
• Save a picture to a .dot file.

Note: If the user loads a picture with 2,000 dots, and enters 100 for the desired number of dots, and subsequently enters 1,000 for the desired number of dots, your program must show a picture with 1,000 dots, not 100.

Details

Changes to Dot Class

You must add the following two methods to the Dot class:

• private static double distance(Dot a, Dot b) that returns the distance between the two dots.
• public static double criticalValue(Dot previous, Dot current, Dot next) that returns the critical value of the current dot as defined below.

Changes to Picture Class

Modify your Picture class so that it only has one attribute of type List and call it dots. This attribute must be declared final. You may not have any references to ArrayLists and LinkedLists.

You must remove all constructors from the Picture class and implement the following constructors:

• Picture(List<Dot> emptyList) — Constructor that uses the list emptyList passed to it to store the dots for this picture.
• Picture(Picture original, List<Dot> emptyList) — Constructor that copies the dots from original into emptyList and uses it to store the dots for this picture.

These constructors provide flexibility in our Picture class because we can now specify the specific implementation of the List used (e.g., ArrayList, LinkedList, or even our own List implementation) by passing the appropriate list to the constructor. In fact, the Picture class is no longer dependent on any concrete list implementation.

You must also implement the following methods in the Picture class:

• void save(Path path) — saves the picture to .dot path that is compatible with the format described in lab 1.
• void keepDots(int numberDesired) — removes all but the numberDesired most critical dots.
  • If the picture does not have more than numberDesired dots, the method returns without changing the picture.
  • If numberDesired < 3, an IllegalArgumentException is thrown.

Your implementation of the keepDots() method must be consistent with this flowchart:

Calculating the Critical Value of a Dot

The critical value of a dot depends on the relative proximity of it and its immediate neighbors. Consider three dots, labeled 1, 2, and 3, on a straight line. If dot 2 is removed, the connect the dots version of the line from 1 to 3 will look exactly the same. Therefore, we can conclude that the dot is not critical. If dot 2 is significantly far from the line connecting dot 1 and 3, then error would be introduced if dot 2 is eliminated, as shown in Figure 3.

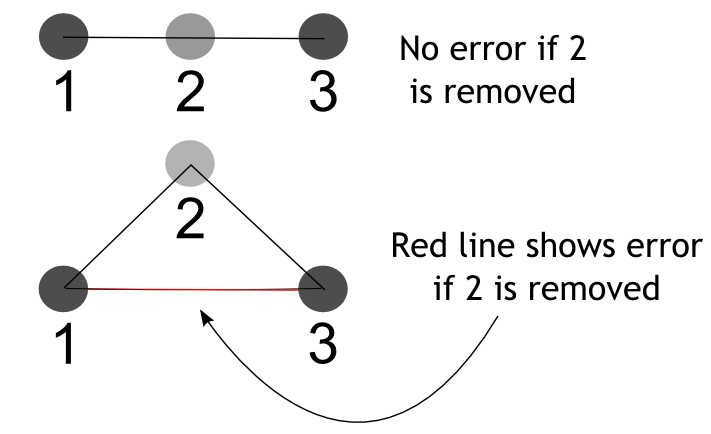
The critical value of dot 2 is calculated as the sum of the distances from dot 2 to dot 1 and from dot 2 to dot 3 minus the distance from dot 1 to dot 3, i.e., \( cv_2 = d_{12} + d_{23} - d_{13} \)

where \( cv_y \) is the critical value for dot \( y \) and \( d_{xz} \) are the distances illustrated below.

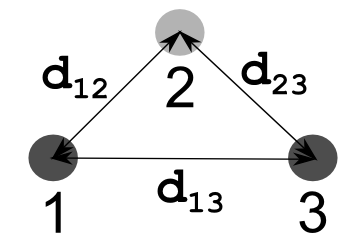
Note that in the case of a straight line between dots 1 and 3, \( cv_2 = 0 \)

Your program should assume that the first and the last dots are connected so they should be treated as neighbors when calculating their critical values.

Exception Handling

There are a number of situations that could cause your program to throw an exception. For example, if the file is not found, cannot be opened, or contains incorrectly formatted data, it is likely that an exception will be thrown. In these cases, the program should display an useful message in an Alert.

Just For Fun

Ambitious students may wish to:

• Try replacing lineTo() with quadraticCurveTo() or bezierCurveTo().
• Add number annotations next to each dot.
• Use shades of colors to indicate the order in which to connect the dots.
• Overlay the reduced-dot picture on top of the picture with all of the dots in the file. You may wish to display the original picture in a lighter color.
• Toggle between the original and reduced-dot pictures with a key press or mouse click.
• Use levels of gray to indicate the critical value of each dot.
• Create a print to PDF option.
• Create an animation that shows the progression of dots being removed from the picture.
• Add a third dimension (x, y, z) to each dot, develop an algorithm for calculating the critical value in 3D, and create a 3D viewer to allow viewing the object from different perspectives.

Acknowledgment

This laboratory assignment, developed by Dr. Chris Taylor, is motivated by the eighth programming project in chapter 2 of our textbook which is based on the paper: L. J. Latecki and R. Lakamper, "Convexity Rule for Shape Decomposition Based on Discrete Contour Evolution," Computer Vision and Image Understanding (CVIU) 73(1999), pp. 441-454.